Hoy vamos a hablar de la hipótesis de Riemann. Es otro de los problemas del milenio y, en nuestro caso, del segundo que hableremos después de P vs NP. Para ponernos en antecedentes, hablaremos primero de Georg Friedrich Bernhard Riemann, uno de los más afamados (y talentosos) matemáticos de la historia moderna.
Riemann (Breselenz, Alemania, 17 de septiembre de 1826 – Verbania, Italia, 20 de julio de 1866) fue un matemático alemán que realizó contribuciones muy importantes en análisis y geometría diferencial; algunas de ellas allanaron el camino para el desarrollo más avanzado de la relatividad general. Su nombre está conectado con la función zeta, la integral de Riemann, el lema de Riemann, las variedades de Riemann, las superficies de Riemann y la geometría de Riemann.
Nació en Breselenz, una aldea cercana a Dannenberg en el Reino de Hanóver, actualmente parte de Alemania. Su padre Friedrich Bernhard Riemann era pastor luterano en Breselenz y había luchado en las guerras napoleónicas. Bernhard era el segundo de seis niños, su frágil salud y la temprana muerte de casi todos sus hermanos fueron debidos a la subalimentación en su juventud. Su madre también murió antes de que sus hijos crecieran.
En 1840 Bernhard fue a Hanóver a vivir con su abuela y a visitar el Lyceum. Después de la muerte de su abuela en 1842 entró al Johanneum Lüneburg. Desde pequeño demostró una fabulosa capacidad para el cálculo unido a una timidez casi enfermiza. Durante sus estudios de secundaria aprendía tan rápido que enseguida adelantaba a todos sus profesores.
En 1846, a la edad de 19, comenzó a estudiar filología y teología en la Universidad de Göttingen, su idea era complacer a su padre y poder ayudar a su familia haciéndose pastor. Atendió a conferencias de Gauss sobre el Método de mínimos cuadrados. En 1847 su padre reunió el dinero suficiente para que comenzara a estudiar matemáticas.
En 1847 se trasladó a Berlín, donde enseñaban Jacobi, Dirichlet y Steiner. En 1848 estallaron manifestaciones y movimientos obreros por toda Alemania, Riemann fue reclutado por las milicias de estudiantes, incluso ayudó a proteger al rey en su palacio de Berlín. Permaneció allí por dos años y volvió a Göttingen en 1849.
En 1859 formuló por primera vez la hipótesis de Riemann, que es uno de los más famosos e importantes problemas sin resolver de las matemáticas (del que hablaremos a continuación)
Riemann dio sus primeras conferencias en 1854, en las cuales fundó el campo de la geometría de Riemann. Lo promovieron a profesor extraordinario en la universidad de Göttingen en 1857 y se hizo profesor ordinario en 1859. En 1862 se casó con Elise Koch. Murió de tuberculosis en su tercer viaje a Italia en Selasca.
El hecho es que salió de Alemania huyendo de los problemas de la época en su país y a las tres semanas de llegar a Italia murió de tuberculosis. Su temprana muerte nos privó de la resolución de su hipótesis, la cual se cree que se encontraba en un estado muy avanzado. El exceso de celo por parte del personal de limpieza de su casa, contribuyó a la destrucción de multitud de documentos, entre los que se encontraban sin duda los referentes a su hipótesis.
Ciento cincuenta y dos años (152) después de su formulación, la hipótesis sigue sin resolución aparente. Actualmente existen multitud de estudios sobre ella; los mejores matemáticos actuales siguen sin encontrar un punto válido para demostrar (o refutar) la hipótesis.
Ahora, creo que estamos en situación de hablar sobre la hipótesis de Riemann. Adelanto que quizás el lenguaje sea un poco farragoso; intentaré solucionarlo en la medida de lo posible.
El enunciado es el siguiente:
La hipótesis de Riemann dice que todos los ceros no triviales de la función zeta de Riemann tienen una parte real de 1/2.
Dicho esto, debemos introducir brevemente qué es la función zeta de Riemann, que son los ceros no triviales y, por último, hablaremos de la propia hipótesis en si.
FUNCION ZETA DE RIEMANN
Se trata de una función que tiene una importancia significativa en la teoría de números, por su relación con la distribución de los números primos. También tiene aplicaciones en otras áreas tales como la física, la teoría de probabilidades y estadística aplicada.
La función zeta de Riemann ζ(s) está definida, para valores reales mayores que 1, por la serie de Dirichlet:

En la región {s ∈ C | Re(s) > 1}, esta serie infinita converge y define una función que es analítica en esta región. Riemann observó que la función zeta puede extenderse de manera única por continuación analítica a una función meromorfa en todo el plano complejo con un único polo en s = 1. Esta es la función que se considera en la hipótesis de Riemann.
Para los complejos con Re(s)<1, los valores de la función deben ser calculados mediante su ecuación funcional, obtenida a partir de la continuación analítica de la función.
La conexión entre esta función y los números primos fue observada por primera vez por Leonhard Euler, que se dio cuenta de que:
Puesto que para cada primo p,  es una serie geométrica, convergente para cualquier número complejo s con Re(s) > 1 a:
es una serie geométrica, convergente para cualquier número complejo s con Re(s) > 1 a:
se obtiene que:
donde el producto infinito es sobre todos los números primos y s un número complejo con Re(s) > 1. Esta expresión es llamada producto de Euler, en honor a su descubridor. La fórmula es consecuencia de dos resultados simples pero fundamentales en Matemática: la fórmula para las series geométricas y el teorema fundamental de la aritmética.
El valor de la función zeta para los números pares negativos es 0 (viendo la ecuación funcional es evidente), por lo que son llamados ceros triviales. Aparte de los ceros triviales, la función también se anula en valores de s que están dentro del rango {s ∈ C: 0 < Re(s) < 1}, y que son llamados ceros no triviales, debido a que es más difícil demostrar la ubicación de esos ceros dentro del rango crítico. El estudio de la distribución de estos «ceros no triviales» es muy importante, debido a que tiene profundas implicaciones en la distribución de los números primos y en cuestiones relacionadas con la teoría de números. La hipótesis de Riemann, asegura que cualquier cero no trivial tiene que Re(s)=1/2, por lo tanto, todos los ceros están alineados en el plano complejo formando una recta, llamada recta crítica.
La localización de estos ceros tiene significativa importancia en teoría de números, ya que, por ejemplo, el hecho de que todos los ceros estén en el rango crítico demuestra el teorema de los números primos. Un mejor resultado es que ζ(σ + it) ≠ 0 para cualquier |t| ≥ 3 y
También es conocido que existen infinitos ceros sobre la recta crítica, como mostraron G.H. Hardy y Littlewood.
Para no complicar esto demasiado (si es que ya no lo está :)) dejaremos en este punto la explicación de la función zeta de Riemann. Considero que tenemos suficiente información para pasar al siguiente punto.
CEROS NO TRIVIALES
Hemos hablado sobre ellos en la función zeta, ahora intentaremos ampliar la información.
En matemática, el término trivial se usa frecuentemente para los objetos (por ejemplo, cuerpos o espacios topológicos) que tienen una estructura muy simple. Para los no matemáticos, son a veces más difíciles de visualizar o entender que otros objetos más complicados. También se usa el término trivial para referirse a una opción, caso o posibilidad poco interesante o exenta de interés pero que debe mencionarse por un afán de completitud.
Algunos ejemplos de los objetos incluyen:
- Conjunto vacío (el conjunto que no contiene elementos)
- Grupo trivial (el grupo matemático que contiene sólo el elemento identidad)
También, trivial se refiere a soluciones (a una ecuación) que tienen una estructura muy simple, pero que por completitud no pueden ser ignoradas. Estas soluciones se denominan soluciones triviales. Por ejemplo, considérese la ecuación diferencial
- y‘ = y
donde y = f(x) es una función cuya derivada es y′. Entonces tenemos la solución trivial
- y = 0, la función cero
y la solución no trivial
- y = ex, la función exponencial.
De igual forma, se suele oír que el último teorema de Fermat descrito como enunciando no contiene soluciones no triviales a la ecuación an + bn = cn cuando n es mayor que 2. Claramente hay algunas soluciones a la ecuación. Por ejemplo, a = b = c = 0 es una solución para cualquier n, tal como a = 1, b = 0, c = 1. Pero dichas soluciones son obvias y sin interés, por tanto “triviales”.
Bien, creo que, al igual que en el caso de la función zeta, ya tenemos bastante información sobre el término trivial en matemática, por lo que podemos pasar al siguiente punto, la hipótesis en si.
HIPOTESIS DE RIEMANN
Recordemos que la hipótesis de Riemann conjetura sobre sobre la distribución de los ceros de la función zeta de Riemann ζ(s).
La hipótesis de Riemann, por su relación con la distribución de los números primos en el conjunto de los naturales, es uno de los problemas abiertos más importantes en la matemática contemporánea.
Se ha ofrecido un premio de un millón de dólares por el Instituto Clay de Matemáticas para la primera persona que desarrolle una demostración correcta de la conjetura. La mayoría de la comunidad matemática piensa que la conjetura es cierta, aunque otros grandes matemáticos como J. E. Littlewood y Atle Selberg se mostraron escépticos, si bien el escepticismo de Selberg fue disminuyendo desde sus días de juventud. En un artículo en 1989 sugirió que un análogo debe ser cierto para una clase mucho más amplia de funciones (la clase de Selberg).
Mencionamos de nuevo que la función zeta de Riemann ζ(s)está definida de la siguiente manera:
Para todos los números complejos s ≠ 1, se puede prolongar analíticamente mediante la ecuación funcional:

Ésta posee ciertos valores, llamados ceros “triviales” para los cuales la función zeta se anula. De la ecuación se puede ver que s = −2, s = −4, s = −6, … son ceros triviales. Existen otros valores complejos s comprendidos entre 0 < Re(s) < 1, para los cuales la función zeta también se anula, llamados ceros “no triviales”. La conjetura de Riemann hace referencia a éstos ceros no triviales afirmando:
La parte real de todo cero no trivial de la función zeta de Riemann es 1/2.
Por lo tanto los ceros no triviales deberían encontrarse en la línea crítica s = 1/2 + i t donde t es un número real e i es la unidad imaginaria. La función zeta de Riemann, a lo largo de la línea crítica ha sido estudiada en términos de la función Z, cuyos ceros corresponden a los ceros de la función zeta sobre la línea crítica.
Riemann mencionó la conjetura, que sería llamada la hipótesis de Riemann, en su artículo de 1859 Sobre los números primos menores que una magnitud dada, al desarrollar una fórmula explícita para calcular la cantidad de primos menores que x. Puesto que no era esencial para el propósito central de su artículo, no intentó dar una demostración de la misma. Riemann sabía que los ceros no triviales de la función zeta están distribuidos en torno a la recta s = 1/2 + i t, y sabía también que todos los ceros no triviales debían estar en el rango 0 ≤ Re(s) ≤ 1.
En 1896, Hadamard y de la Vallée-Poussin probaron independientemente, que ningún cero podía estar sobre la recta Re(s) = 1. Junto con las otras propiedades de los ceros no triviales demostradas por Riemann, esto mostró que todos los ceros no triviales deben estar en el interior de la banda crítica 0 < Re(s) < 1. Este fue un paso fundamental para las primeras demostraciones del teorema de los números primos.
En 1900, Hilbert incluyó la hipótesis de Riemann en su famosa lista de los 23 problemas no resueltos (es parte del problema 8 en la lista de Hilbert junto con la conjetura de Goldbach). Cuando se le preguntó qué haría si se despertara habiendo dormido quinientos años, remarcablemente Hilbert contestó que su primera pregunta sería si la hipótesis de Riemann había sido probada. La hipótesis de Riemann es el único problema de los que propuso Hilbert que está en el premio del milenio del Instituto Clay de Matemáticas.
En 1914, Hardy demostró que existe un número infinito de ceros sobre la recta crítica Re(s) = 1/2. Sin embargo todavía era posible que un número infinito (y posiblemente la mayoría) de los ceros no triviales se encontraran en algún otro lugar sobre la banda crítica. En trabajos posteriores de Hardy y Littlewood en 1921 y de Selberg en 1942 se dieron estimaciones para la densidad promedio de los ceros sobre la línea crítica.
Trabajos recientes se han concentrado en el cálculo explícito de la localización de grandes cantidades de ceros (con la esperanza de hallar algún contraejemplo) y en el establecimiento de cotas superiores en la proporción de ceros que puedan estar lejos de la línea crítica (con la esperanza de reducirlas a cero).
La formulación tradicional de la hipótesis de Riemann oscurece un poco la importancia real de la conjetura. La función zeta de Riemann tiene una profunda conexión con los números primos y Hege von Koch demostró en 1901 que la hipótesis de Riemann es equivalente al considerable refinamiento del teorema de los números primos: Existe una constante C > 0 tal que

para todo x suficientemente grande, donde π(x) es la función contadora de primos y ln(x) es el logaritmo natural de x. Lowell Schoenfeld mostró que se puede tomar C = 1/(8 π) para todo x ≥ 2657.
Los ceros de la función zeta y los números primos satisfacen ciertas propiedades de dualidad, conocidas como fórmulas explícitas, que muestran, usando análisis de Fourier, que los ceros de la función zeta de Riemann pueden interpretarse como frecuencias armónicas en la distribución de los números primos.
Más aún, si la conjetura de Hilbert-Polya es cierta, entonces cualquier operador que nos dé las partes imaginarias de los ceros como sus valores propios debe satisfacer:
donde Tr es la traza del operador (suma de sus valores propios) , β es un número imaginario y ψ(x) es la Función de Chebyshov que nos suma el log(x) sobre los primos y sus potencias enteras. Dicha fórmula es una conclusión de la ‘fórmula explicita’ de V. Mangoldt. Varios operadores propuestos por C. Perelman, J. Macheca y J. Garcia, parecen corroborar los resultados de la conjetura de Hilbert sobre el operador, reproduciendo la parte imaginaria de los ceros. Usando la teoría WKB o de Cuantizacion de Bohr-Sommerfeld uno puede probar que si el potencial V(x) de un Hamiltoniano H cuyas energías sean las partes imaginarias de los ceros no triviales debe cumplir (ecuación implícita)  donde N(T) es el número de ceros con parte imaginaria menor que un dado T >0 y
donde N(T) es el número de ceros con parte imaginaria menor que un dado T >0 y  significa la derivada fraccional de orden 1/2.
significa la derivada fraccional de orden 1/2.
Por último, podemos añadir en cálculo numérico los siguientes logros:
- En el año 2004 Xavier Gourdon verificó la conjetura de Riemann numéricamente a lo largo de los primeros diez trillones de ceros no triviales de la función. Sin embargo esto no es estrictamente una demostración, numéricamente es más interesante encontrar un contraejemplo, es decir un valor de cero que no cumpla con que su parte real es 1/2, pues esto echaría por los suelos la validez de la conjetura.
- Hasta el año 2005, el intento más serio para explorar los ceros de la función-ζ, es el ZetaGrid, un proyecto de computación distribuida con la capacidad de verificar billones de ceros por día. El proyecto acabó en diciembre de 2005,y ninguno de los ceros pudo ser identificado como contraejemplo de la hipótesis de Riemann.
Y esto es todo amigos!!! Espero (aunque no estoy seguro de haberlo conseguido) que todos hayamos podido entender en qué consiste la hipótesis de Riemann y cuáles son sus consecuencias. Al contrario que sucede con P vs NP, toda la comunidad científica internacional da por válida la hipótesis, es más, muchas otras (como la conjetura de Goldbach), también quedarían demostradas por ende. Recordar que la conjetura de Goldbach enuncia lo siguiente:
Todo número par mayor que 2 puede expresarse como suma de dos números primos.
Esto fue enunciado por Christian Goldbach en 1742 y al igual que con la hipótesis de Riemann nunca ha sido demostrado (corroborado o refutado). En cuanto a las consecuencias para la hipótesis de Riemann (de ser cierta o no), bueno, podríamos decir muchas cosas, pero lo más importante es que si fuera cierta y pudiéramos demostrarla, todos los sistemas de encriptación actuales quedarían obsoletos, ya que se basan en los primos, o expresado de otra forma, en la sucesión de cifras dadas a partir de dos primos originales. Con los métodos computacionales actuales, dar con esos dos números originales es prácticamente imposible, pero claro, esto dejaría de ser así si se demostrara la hipótesis de Riemann. No obstante, la matemática actual se basa en gran medida o está relacionadad directa o indirectamente con la hipótesis de Riemann, así que más nos vale a todos que sea cierta.
Os recomiendo encarecidamente el documental de la BBC “the music of primes” presentado y dirigido por el profesor de matemáticas de la Universidad de Oxford Marcus Peter Francis du Sautoy (también existe el libro) Se trata de un bello y excelente informe en modo documental y en tres capítulos sobre los números primos, la hipótesis de Riemann y el mundo matemático.
Espero que hayáis disfrutado leyendo este informe tanto como yo redactándolo. A continuación detallo las referencias consultadas para la redacción de este artículo y os dejo el texto original de Riemann (traducido al inglés):
EZeta (on the number of prime numbers less than a given quantity)
Bombieri, Enrico (2000) The Riemann Hypothesis – official problem description, Clay Mathematics Institute.
The Millennium Prize Problems (http://www.claymath.org/millennium)
Riemann, Bertrand (1859). “Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse”
Explicit formula http://www.wbabin.net/science/moreta8.pdf
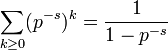



![\sum_{n}e^{-\beta E_{n}}=Tr[e^{-\beta \hat H}]=e^{u/2}-e^{-u/2} \frac{d\psi _{0}}{du}-\frac{e^{u/2}}{e^{3u}-e^{u}},](https://i0.wp.com/upload.wikimedia.org/math/0/8/4/084a91626171144d3b39500d69487a8a.png)