Mecánica cuántica y orbitales atómicos

Description : Erwin Schrödinger, Austrian phys... — Image via Wikipedia

Buenas …. ya estoy aquí de nuevo para dar un poco la tabarra con la mecánica cuántica. Básicamente tengo un problema con ella, bueno … dos. Uno es que la base matemática de la mecánica cuántica es extremadamente complicada. El segundo problema es que, a pesar de salvar el problema matemático, sigo sin entender nada 🙂

A ver, el tema puede sonar un poco complicado de entender. Ya publiqué un post sobre la mecánica cuántica, en inglés y hablando en términos generales. Ahora me centraré en los orbitales atómicos … pero … ¿qué son los orbitales atómicos?

Un orbital atómico es una determinada solución particular, espacial e independiente del tiempo a la ecuación de Schrödinger para el caso de un electrón sometido a un potencial coulombiano. La elección de tres números cuánticos en la solución general señalan unívocamente a un estado monoelectrónico posible.

Estos tres números cuánticos hacen referencia a la energía total del electrón, el momento angular orbital y la proyección del mismo sobre el eje z del sistema del laboratorio y se denotan por:

$\langle\vec{r}|nlm\rangle=\psi_{n,l}^{m}(\vec r)$

El nombre de orbital también atiende a la función de onda en representación de posición independiente del tiempo de un electrón en una molécula. En este caso se utiliza el nombre orbital molecular.

La combinación de todos los orbitales atómicos dan lugar a la corteza electrónica representado por el modelo de capas electrónico. Este último se ajusta a los elemento según la configuración electrónica correspondiente.

Vale, ahora ya sabemos que es un orbital atómico y orbital molecular pero … ¿qué es la ecuación de Schrödinger?

La ecuación de Schrödinger fue desarrollada por el físico austríaco Erwin Schrödinger en 1925. Describe la evolución temporal de una partícula masiva no relativista. Es de importancia central en la teoría de la mecánica cuántica, donde representa para las partículas microscópicas un papel análogo a la segunda ley de Newton en la mecánica clásica. Las partículas microscópicas incluyen a las partículas elementales, tales como electrones, así como sistemas de partículas, tales como núcleos atómicos.

Bien y ¿cómo es la formulación de la ecuación de Schrödinger?

En mecánica cuántica, el estado en el instante t de un sistema se describe por un elemento $\left| \Psi (t)\right\rangle$ del espacio complejo de Hilbert — usando la notación bra-ket de Paul Dirac. $\left| \Psi (t)\right\rangle$ representa las probabilidades de resultados de todas las medidas posibles de un sistema.

La evolución temporal de $\left| \Psi (t)\right\rangle$ se describe por la ecuación de Schrödinger :

$\mathbf{\hat{H}} \left| \Psi (t)\right\rangle = i \hbar {d\over dt} \left| \Psi (t) \right\rangle = \frac{\hat{\vec{\mathbf{p}}}^2}{2m}\left| \Psi (t)\right\rangle + V(\hat{\vec{\mathbf{r}}},t)\left| \Psi (t) \right\rangle$

donde:

$i\,$ : es la unidad imaginaria ;
$\hbar\,$ : es la constante de Planck normalizada (h/2π) ;
$\hat{H}\,$ : es el hamiltoniano, dependiente del tiempo en general, el observable corresponde a la energía total del sistema ;
$\hat{\vec{\mathbf{r}}}\,$ : es el observable posición ;
$\hat{\vec{\mathbf{p}}}\,$ : es el observable impulso.

¿Veis lo que os decía con la parte matemática de la mecánica cuántica?

Ahora, después de haber introducido en sociedad a los orbitales atómicos, podemos hablar de ellos con más propiedad.

En el año 1927, E. Schorödinger (Premio Nobel de Física 1933) apoyándose en el concepto de dualidad onda-corpúsculo enunciado por Louis de Broglie (Premio Nobel de Fisica 1929), formula la Mecánica Ondulatoria y, Werner Heisenberg (Premio Nobel de Física 1932) -NOTA: VAYA TRES!-, la Mecánica de Matrices. Ambas mecánicas inician un nuevo camino en el conocimiento de la estructura atómica, y ampliadas por Born, Jordan, Dirac y otros has dado lugar a lo que actualmente se denomina Mecánica Cuántica. Frente al determinismo de la mecánica clásica, la mecánica cuántica es esencialmente probabilística y utiliza un aparato matemático más complejo y complicado que la mecánica clásica (yo doy fe de ello). Actualmente, el modelo atómico que se admite es el modelo propuesto por la mecánica cuántica (modelo de Schrödinger).

El modelo de Bohr es un modelo unidimensional que utiliza un número cuántico (n) para describir la distribución de electrones en el átomo. El modelo de Schrödinger permite que el electrón ocupe un espacio tridimensional. Por lo tanto requiere tres números cuánticos para describir los orbitales en los que se puede encontrar al electrón. La descripción del átomo mediante la mecánica ondulatoria está basada en el cálculo de las soluciones de la ecuación de Schrödinger; está es una ecuación diferencial que permite obtener los números cuánticos de los electrones.

es la llamada función de onda. Contiene la información sobre la posición del electrón. También se denomina orbital, por analogía con las órbitas de los modelos atómicos clásicos.

El cuadrado de la función de onda |2, es la llamada densidad de probabilidad relativa del electrón y representa la probabilidad de encontrar al electrón en un punto del espacio (x, y, z).

E es el valor de la energía total del electrón.

V representa la energía potencial del electrón un punto (x, y, z). Por tanto, E-V es el valor de la energía cinética cuando el electrón está en el punto (x, y, z).

Las soluciones, o funciones de onda, , son funciones matemáticas que dependen de unas variables que sólo pueden tomar valores enteros. Estas variables de las funciones de onda se denominan números cuánticos: número cuántico principal, (n), angular (l) y número cuántico magnético (m_l). Estos números describen el tamaño, la forma y la orientación en el espacio de los orbitales en un átomo.

El número cuántico principal (n) describe el tamaño del orbital, por ejemplo: los orbitales para los cuales n=2 son más grandes que aquellos para los cuales n=1. Puede tomar cualquier valor entero empezando desde 1: n=1, 2, 3, 4, etc.

El número cuántico del momento angular orbital (l) describe la forma del orbital atómico. Puede tomar valores naturales desde 0 hasta n-1 (siendo n el valor del número cuántico principal). Por ejemplo si n=5, los valores de l pueden ser: l= 0, 1 ,2, 3, 4. Siguiendo la antigua terminología de los espectrocopistas, se designa a los orbitales atómicos en función del valor del número cuántico secundario, l, como:

l = 0 orbital s (sharp)

l = 1 orbital p (principal)

l = 2 orbital d (diffuse)

l = 3 orbital f (fundamental)

El número cuántico magnético (m_l), determina la orientación espacial del orbital. Se denomina magnético porque esta orientación espacial se acostumbra a definir en relación a un campo magnético externo. Puede tomar valores enteros desde -l hasta +l. Por ejemplo, si l=2, los valores posibles para m son: m_l=-2, -1, 0, 1, 2.

El número cuántico de espín (s), sólo puede tomar dos valores: +1/2 y -1/2.

Todos los orbitales con el mismo valor del número cuántico principal, n, se encuentran en la misma capa electrónica principal o nivel principal, y todos los orbitales con los mismos valores de n y l están en la misma subcapa o subnivel.

El número de subcapas en una capa principal es igual al número cuántico principal, esto es, hay una subcapa en la capa principal con n=1, dos subcapas en la capa principal con n=2 y así sucesivamente. El nombre dado a una subcapa, independientemente de la capa principal en la que se encuentre, está determinado por el número cuántico l, de manera que como se ha indicado anteriormente: l=0 (subcapa s), l=1 (subcapa p), l=2 (subcapa d) y l=3 (subcapa f).

El número de orbitales en una subcapa es igual al número de valores permitidos de m_l para un valor particular de l, por lo que el número de orbitales en una subcapa es 2l+1. Los
nombres de los orbitales son los mismos que los de las subcapas en las que aparecen.

orbitales s	orbitales p	orbitales d	orbitales f
*l=0*	*l=1*	*l=2*	*l=3*
*m_l=0*	m_l=-1, 0, +1	m_l=-2, -1, 0, +1, +2	m_l=-3, -2, -1, 0, +1, +2, +3
un orbital s en una subcapa s	tres orbitales p en una subcapa p	cinco orbitales d en una subcapa d	siete orbitales f en una subcapa f

La imagen de los orbitales empleada habitualmente por los químicos consiste en una representación del orbital mediante superficies límite que engloban una zona del espacio donde la probabilidad de encontrar al electrón es del 99%. La extensión de estas zonas depende básicamente del número cuántico principal, n, mientras que su forma viene determinada por el número cuántico secundario, l.

Los orbitales s (l=0) tienen forma esférica. La extensión de este orbital depende del valor del número cuántico principal, así un orbital 3s tiene la misma forma pero es mayor que un orbital 2s.

Los orbitales p (l=1) están formados por dos lóbulos idénticos que se proyectan a lo largo de un eje. La zona de unión de ambos lóbulos coincide con el núcle atómico. Hay tres orbitales p (m=-1, m=0 y m=+1) de idéntica forma, que difieren sólo en su orientación a lo largo de los ejes x, y ó z.

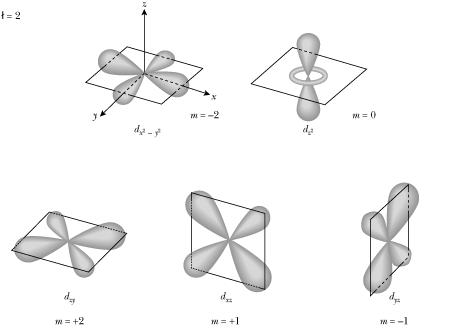
Los orbitales d (l=2) también están formados por lóbulos. Hay cinco tipos de orbitales d (que corresponden a m=-2, -1, 0, 1, 2)

Los orbitales f (l=3) también tienen un aspecto multilobular. Existen siete tipos de orbitales f (que corresponden a m=-3, -2, -1, 0, +1, +2, +3).

Una vez descritos los cuatro número cuánticos, podemos utilizarlos para describir la estructura electrónica del átomo de hidrógeno:

El electrón de un átomo de hidrógeno en el estado fundamental se encuentra en el nivel de energía más bajo, es decir, n=1 y, dado que la primera capa principal contiene sólo un orbital s, el número cuántico orbital es l=0. El único valor posible para el número cuántico magnético es m_l=0. Cualquiera de los dos estados de spin son posibles para el electrón.

Así podríamos decir que el electrón de un átomo de hidrógeno en el estado fundamental está en el orbital 1s, o que es un electrón 1s, y se representa mediante la notación:

1s¹

en donde el superíndice 1 indica un electrón en el orbital 1s. Ambos estados de espín están permitidos, pero no designamos el estado de espín en esta notación.

La resolución de la ecuación de Schrödinger para átomos con más de un electrón es un proceso matemático muy complejo que obliga a realizar cálculos aproximados. En los átomos multielectrónicos aparece un nuevo factor: las repulsiones mutuas entre los electrones. Este hecho se traduce en que los electrones en un átomo multielectrónico tratan de permanecer alejados de los demás y sus movimientos se enredan mutuamente.

Escribir la configuración electrónica de un átomo consiste en indicar cómo se distribuyen sus electrones entre los diferentes orbitales en las capas principales y las subcapas. Muchas de las propiedades físicas y químicas de los elementos pueden relacionarse con las configuraciones electrónicas.

Esta distribución se realiza apoyándonos en tres reglas: energía de los orbitales, principio de exclusión de Pauli y regla de Hund.

Los electrones ocupan los orbitales de forma que se minimice la energía del átomo. El orden exacto de llenado de los orbitales se estableció experimentalmente, principalmente mediante estudios espectroscópicos y magnéticos y es el orden que debemos seguir al asignar las configuraciones electrónicas a los elementos. El orden de llenado de orbitales es como sigue:

1s²2s²2p⁶3s²3p⁶4s²3d¹⁰4p⁶5s²4d¹⁰5p⁶6s²4f¹⁴5d¹⁰6p⁶7s²5f¹⁴6d¹⁰7p⁶

Para recordar este orden más facilmente se puede utilizar el diagrama siguiente:

Empezando por la línea superior, sigue las flechas y el orden obtenido es el mismo que en la serie anterior. Debido al límite de dos electrones por orbital, la capacidad de una subcapa de electrones puede obtenerse tomanto el doble del número de orbitales en la subcapa. Así, la subcapa s consiste en un orbital con una capacidad de dos electrones; la subcapa p consiste en tres orbitales con una capacidad total de seis electrones; la subcapa d consiste en cinco orbitales, con una capacidad total de diez electrones; la subcapa f consiste en siete orbitales con una capacidad total de catorce electrones.

En un determinado átomo los electrones van ocupando, y llenando, los orbitales de menor energía; cuando se da esta circunstancia el átomo se encuentra en su estado fundamental. Si el átomo recibe energía, alguno de sus electrones más externos pueden saltar a orbitales de mayor energía, pasando el átomo a un estado excitado.

Principio de exclusión de Pauli. En un átomo no puede haber dos electrones con los cuatro número cuánticos iguales.

Los tres primeros número cuánticos, n, l y m_l determinan un orbital específico. Dos electrones, es un átomo, pueden tener estos tres números cuánticos iguales, pero si es así, deben tener valores diferentes del número cuántico de espín. Podríamos expresar esto diciendo lo siguiente: un orbital solamente puede estar ocupado por dos electrones y estos electrones deben tener espines opuestos.

Regla de Hund. Al llenar orbitales de igual energía (los tres orbitales p, los cinco orbitales
d, o los siete orbitales f los electrones se distribuyen, siempre que sea posible, con sus espines paralelos, es decir, despareados.

Por ejemplo, La estructura electrónica del ₇N es: 1s² 2s² 2p_x¹ 2p_y¹ 2p_z¹ .

Para escribir las configuraciones electrónicas utilizaremos el principio aufbau. Aufbau es una palabra alemana que significa “construcción progresiva”; utilizaremos este método para asignar las configuraciones electrónicas a los elementos por orden de su número atómico creciente. Veamos por ejemplo como sería la configuración electrónica para Z=11-18, es decir, desde Na hasta el Ar.

Cada uno de estos elementos tiene las subcapas 1s, 2s y 2p llenas. Como la configuración 1s²2s²2p⁶ corresponde a la del neón, la denominamos “configuración interna del neón” y la representamos con el símbolo químico del neón entre corchetes, es decir, [Ne]. Los electrones que se situan en la capa electrónica del número cuántico principal más alto, los más exteriores, se denominan electrones de valencia. La configuración electrónica del Na se escribe en la forma denominada “configuración electrónica abreviada interna del gas noble” de la siguiente manera:

Na: [Ne]3s¹ (consta de [Ne] para la configuración interna del gas noble y 3s¹ para la configuración del electrón de valencia.

De manera análoga, podemos escribir la configuración electrónica para Mg, Al, Si, P…

Mg: [Ne]3s²

Al: [Ne]3s²3p¹

Si: [Ne]3s²3p²

P: [Ne]3s²3p³

S: [Ne]3s²3p⁴

Cl: [Ne]3s²3p⁵

Ar: [Ne]3s²3p⁶

Y ahora, un par de ejercicios sobre todo lo aquí escrito con su resolución.

1.- Escribir la estructura electrónica del P (Z=15) aplicando la regla de máxima multiplicidad de Hund.

₁₅P es: 1s² 2s² 2p⁶ 3s² 3p³ (3p_x¹ 3p_y¹ 3p_z¹ )

2.- Escribir la estructura electrónica del Sc (Z=21) mediante la configuración abreviada interna del gas noble.

Sc: [Ar]4s²3d¹

Bueno, pues con esto terminamos por hoy … Espero que encontréis este artículo de utilidad y que seáis felices … Por mi parte, seguiré estudiando. Sed buenos 🙂